10.16 Intro to Data Science: Time Series and Simple Linear Regression

  • Time series: Sequences of values (observations) associated with points in time
    • daily closing stock prices
    • hourly temperature readings
    • changing positions of a plane in flight
    • annual crop yields
    • quarterly company profits
    • time-stamped tweets from Twitter users worldwide
  • We’ll use simple linear regression to make predictions from time series data

Time Series

  • Univariate time series: One observation per time
  • Multivariate time series: Two or more observations per time
  • Two tasks often performed with time series are:
    • Time series analysis, which looks at existing time series data for patterns (like seasonality), helping data analysts understand the data
    • Time series forecasting, which uses past data to predict the future
  • We’ll perform time series forecasting

Simple Linear Regression

  • Given a collection of values representing an independent variable (the month/year combination) and a dependent variable (the average high temperature for that month/year), simple linear regression describes the relationship between these variables with a straight line, known as the regression line

Linear Relationships

  • Given a Fahrenheit temperature, we can calculate the corresponding Celsius temperature using:
    c = 5 / 9 * (f - 32)
  • f (the Fahrenheit temperature) is the independent variable
  • c (the Celsius temperature) is the dependent variable
  • Each value of c depends on the value of f used in the calculation

Linear Relationships (cont.)

  • Plotting Fahrenheit temperatures and their corresponding Celsius temperatures produces a straight line
In [1]:
# enable high-res images in notebook 
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
c = lambda f: 5 / 9 * (f - 32)
In [2]:
temps = [(f, c(f)) for f in range(0, 101, 10)]
  • Place the data in a DataFrame, then use its plot method to display the linear relationship between the temperatures
  • style keyword argument controls the data’s appearance
    • '.-' indicates that each point should appear as a dot, and that lines should connect the dots
In [3]:
import pandas as pd
In [4]:
temps_df = pd.DataFrame(temps, columns=['Fahrenheit', 'Celsius'])
In [5]:
axes = temps_df.plot(x='Fahrenheit', y='Celsius', style='.-')
y_label = axes.set_ylabel('Celsius')

Components of the Simple Linear Regression Equation

The points along any straight line can be calculated with:

\begin{equation} y = m x + b \end{equation}
  • m is the line’s slope,
  • b is the line’s `intercept with the y-axis (at x = 0),
  • x is the independent variable (the date in this example)
  • y is the dependent variable (the temperature in this example)
  • In simple linear regression, y is the predicted value for a given x

Function linregress from the SciPy’s stats Module

  • Simple linear regression determines slope (m) and intercept (b) of a straight line that best fits your data
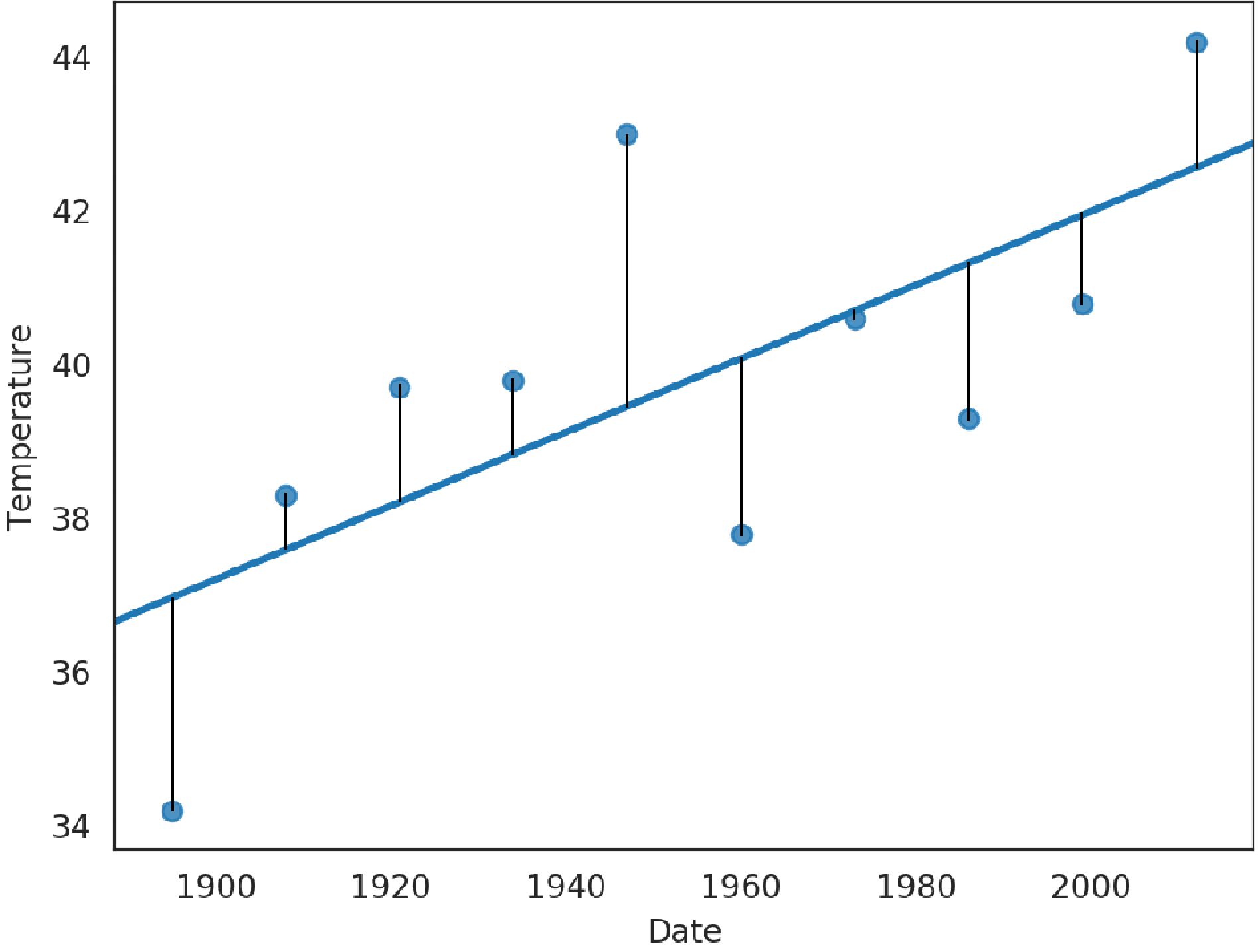
  • Following diagram shows a few of the time-series data points we’ll process in this section and a corresponding regression line
    • We added vertical lines to indicate each data point’s distance from the regression line

A few time series data points and a regression line

Function linregress from the SciPy’s stats Module (cont.)

  • Simple linear regression algorithm iteratively adjusts the slope and intercept and, for each adjustment, calculates the square of each point’s distance from the line
  • “Best fit” occurs when slope and intercept values minimize sum of those squared distances
    • ordinary least squares calculation
  • SciPy (Scientific Python) is widely used for engineering, science and math in Python
    • linregress function (from the scipy.stats module) performs simple linear regression for you

Getting Weather Data from NOAA

  • The National Oceanic and Atmospheric Administration (NOAA) offers public historical data including time series for average high temperatures in specific cities over various time intervals
  • Obtained the January average high temperatures for New York City from 1895 through 2018 from NOAA’s “Climate at a Glance” time series at:

    https://www.ncdc.noaa.gov/cag/

  • ave_hi_nyc_jan_1895-2018.csv in the ch10 examples folder
  • Three columns per observation:
    • Date—A value of the form 'YYYYMM’ (such as '201801'). MM is always 01 because we downloaded data for only January of each year.
    • Value—A floating-point Fahrenheit temperature.
    • Anomaly—The difference between the value for the given date and average values for all dates (not used in this example)

Loading the Average High Temperatures into a DataFrame

In [6]:
nyc = pd.read_csv('ave_hi_nyc_jan_1895-2018.csv')
  • Get a sense of the data
In [7]:
nyc.head()
Out[7]:
Date Value Anomaly
0 189501 34.2 -3.2
1 189601 34.7 -2.7
2 189701 35.5 -1.9
3 189801 39.6 2.2
4 189901 36.4 -1.0
In [8]:
nyc.tail()
Out[8]:
Date Value Anomaly
119 201401 35.5 -1.9
120 201501 36.1 -1.3
121 201601 40.8 3.4
122 201701 42.8 5.4
123 201801 38.7 1.3

Cleaning the Data

  • For readability, rename the 'Value' column as 'Temperature'
In [9]:
nyc.columns = ['Date', 'Temperature', 'Anomaly']
In [10]:
nyc.head(3)
Out[10]:
Date Temperature Anomaly
0 189501 34.2 -3.2
1 189601 34.7 -2.7
2 189701 35.5 -1.9
  • Seaborn labels the tick marks on the x-axis with Date values
  • x-axis labels will be more readable if they do not contain 01 (for January), so we’ll remove it from each Date
  • Check the column’s type:
In [11]:
nyc.Date.dtype
Out[11]:
dtype('int64')
  • Values are integers, so we can divide by 100 to truncate the last two digits
  • Series method floordiv performs integer division on every element of the Series
In [12]:
nyc.Date = nyc.Date.floordiv(100)
In [13]:
nyc.head(3)
Out[13]:
Date Temperature Anomaly
0 1895 34.2 -3.2
1 1896 34.7 -2.7
2 1897 35.5 -1.9

Calculating Basic Descriptive Statistics for the Dataset

  • Call describe on the Temperature column
In [14]:
pd.set_option('precision', 2)
In [15]:
nyc.Temperature.describe()
Out[15]:
count    124.00
mean      37.60
std        4.54
min       26.10
25%       34.58
50%       37.60
75%       40.60
max       47.60
Name: Temperature, dtype: float64

Forecasting Future January Average High Temperatures

  • SciPy (Scientific Python) library widely used for engineering, science and math in Python
  • stats module provides function linregress, which calculates a regression line’s slope and intercept
In [16]:
from scipy import stats
In [17]:
linear_regression = stats.linregress(x=nyc.Date,
                                     y=nyc.Temperature)
  • linregress receives two one-dimensional arrays of the same length representing the data points’ x- and y-coordinates
    • xand y represent the independent and dependent variables, respectively
  • Returns the regression line’s slope and intercept
In [18]:
linear_regression.slope
Out[18]:
0.014771361132966163
In [19]:
linear_regression.intercept
Out[19]:
8.694993233674289
  • Use these values with the simple linear regression equation for a straight line to predict the average January temperature in New York City for a given year
  • In the following calculation, linear_regression.slope is m, 2019 is x (the date value for which you’d like to predict the temperature), and linear_regression.intercept is b:
In [20]:
linear_regression.slope * 2019 + linear_regression.intercept
Out[20]:
38.51837136113297
  • Approximate the average temperature for January of 1890:
In [21]:
linear_regression.slope * 1890 + linear_regression.intercept
Out[21]:
36.612865774980335
  • We had data for 1895–2018
  • The further you go outside this range, the less reliable the predictions will be

Plotting the Average High Temperatures and a Regression Line

  • Seaborn’s regplot function plots each data point with the dates on the x**-axis and the temperatures on the y-axis
  • Creates a scatter plot or scattergram representing the Temperatures for the given Dates and adds the regression line
  • Function regplot’s x and y keyword arguments are one-dimensional arrays of the same length representing the x-y coordinate pairs to plot
In [22]:
import seaborn as sns
In [23]:
sns.set_style('whitegrid')
In [24]:
axes = sns.regplot(x=nyc.Date, y=nyc.Temperature)
axes.set_ylim(10, 70)
Out[24]:
(10, 70)
  • In this graph, the y-axis represents a 21.5-degree temperature range between the minimum of 26.1 and the maximum of 47.6
  • By default, the data appears to be spread significantly above and below the regression line, making it difficult to see the linear relationship
  • Common issue in data analytics visualizations
  • Seaborn and Matplotlib auto-scale the axes, based on the data’s range of values
  • We scaled the y-axis range of values to emphasize the linear relationship

Getting Time Series Datasets

Sources time-series dataset
https://data.gov/
This is the U.S. government’s open data portal. Searching for “time series” yields over 7200 time-series datasets.
https://www.ncdc.noaa.gov/cag/`
The National Oceanic and Atmospheric Administration (NOAA) Climate at a Glance portal provides both global and U.S. weather-related time series.
https://www.esrl.noaa.gov/psd/data/timeseries/
NOAA’s Earth System Research Laboratory (ESRL) portal provides monthly and seasonal climate-related time series.
https://www.quandl.com/search
Quandl provides hundreds of free financial-related time series, as well as fee-based time series.
https://datamarket.com/data/list/?q=provider:tsdl
The Time Series Data Library (TSDL) provides links to hundreds of time series datasets across many industries.
http://archive.ics.uci.edu/ml/datasets.html
The University of California Irvine (UCI) Machine Learning Repository contains dozens of time-series datasets for a variety of topics.
http://inforumweb.umd.edu/econdata/econdata.html
The University of Maryland’s EconData service provides links to thousands of economic time series from various U.S. government agencies.

©1992–2020 by Pearson Education, Inc. All Rights Reserved. This content is based on Chapter 5 of the book Intro to Python for Computer Science and Data Science: Learning to Program with AI, Big Data and the Cloud.

DISCLAIMER: The authors and publisher of this book have used their best efforts in preparing the book. These efforts include the development, research, and testing of the theories and programs to determine their effectiveness. The authors and publisher make no warranty of any kind, expressed or implied, with regard to these programs or to the documentation contained in these books. The authors and publisher shall not be liable in any event for incidental or consequential damages in connection with, or arising out of, the furnishing, performance, or use of these programs.